


Next: Authentication
Up: Some security techniques
Previous: Some security techniques
Modern networks are vulnerable in that an intruder can often
relatively easily gain access to a communications link and eavesdrop
on communications.
An intruder listening in on communications could learn passwords or
other information that enable him to pose as a legal system user.
Other intruders might be satisfied with only stealing information
flowing in the network, or might alter or replace it to gain an
advantage, or cause damage to a competitor. It might, for instance, be
tempting to add two or three zeros to an amount of money being transfered
electronically between two banks, especially for someone having access
to the receiving account.
There are however countermeasures to these threats. These measures
have in common that they all build upon cryptographic techniques.
There are two main cryptographic operations that can be used to
provide secure network communications. A message that is transmitted
can be signed and it can be sealed.
The signature of a signed message is constructed as a checksum
that depends both on the contents of the message and on a
cryptographic key. If the message has been changed in transit, the
signature will no longer match the message, and the alteration can be
detected.
When a message is signed, the contents of the message are not changed
and can thus still be eavesdropped upon. To protect the contents of an
electronic message from prying eyes, the message is put into the
electronic equivalent of a sealed envelope. In the electronic
context, sealing means to make the message itself illegible to
anyone but the intended recipient by encrypting it.
An encryption algorithm is a mathematical function that takes as
input a message, often called plaintext (or sometimes
cleartext), and a key. The output of the function is a new
message called ciphertext. Given the ciphertext, it should be
infeasible to derive the clear text without the key, even if the
enciphering function is known. Neither should it be possible to
deduce the key even if both clear and ciphertext are known.
Cryptographic methods can be divided into two areas according to
how the cryptographic keys are used. Symmetric key cryptography
requires the same key to be known by both the originator and the
recipient. In asymmetric key cryptography, keys come in pairs,
where the originator has one key and the recipient the other. For secrecy
to be maintained, it is paramount that the key needed for
deciphering a message is kept secret.
Ever since ancient times various kinds of codes and ciphers have been
used to protect the confidentiality of sensitive messages should they
fall into wrong hands. These methods have in common that the
original message is transformed in some way using a reversible
process that incorporates a secret that is known only to the
communicating parties.
In encrypted electronic communication the shared secret is a key. The
key is usually just a large number, sizes of 40-128 binary bits are common for symmetric
ciphers. When symmetric encryption algorithms are used, the
same key is used both to encipher and decipher a message. The main
advantage of using this technique is that very fast algorithms and
even hardware implementations are available. This means that
communications can be encrypted without imposing a substantial
overhead.
of 40-128 binary bits are common for symmetric
ciphers. When symmetric encryption algorithms are used, the
same key is used both to encipher and decipher a message. The main
advantage of using this technique is that very fast algorithms and
even hardware implementations are available. This means that
communications can be encrypted without imposing a substantial
overhead.
There are also some disadvantages associated with symmetric key
cryptography. The fact that the key must be available for both
originator and the recipient means that it somehow has to be
transferred, and that that transfer also has to be made securely.
Another security concern is that it is necessary to trust all
possessors of the key not to divulge it to a third party.
In contrast to its symmetric counterpart, asymmetric key cryptography
requires the existence of a pair of keys. One,  , is
usually kept secret whilst the other one,
, is
usually kept secret whilst the other one, 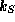 , can be made
public. The keys are so constructed that it is not feasible to derive
the value of one key from the value of the other. Both keys have the
same properties, so which one is kept secret and which is made public is of
no consequence.
, can be made
public. The keys are so constructed that it is not feasible to derive
the value of one key from the value of the other. Both keys have the
same properties, so which one is kept secret and which is made public is of
no consequence.
If we denote the encryption 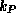 , and the decryption
, and the decryption 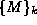 ,
of a message M, using a key k, the properties of the
asymmetric keys
,
of a message M, using a key k, the properties of the
asymmetric keys  and
and 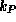 can be expressed as:
can be expressed as: 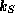 . An important property,
however, is that for any key k of
. An important property,
however, is that for any key k of  and
and 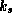 it holds
that
it holds
that 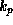 .
.
The great advantage of asymmetric key cryptography is that no secret
key has to be transferred to another party. On the other hand,
asymmetric key cryptography is computationally costly. For this reason
a common use of asymmetric key cryptography is to securely exchange a
symmetric one-time secret key between communicating parties.
An additional advantage of this method is that asymmetric cryptography
also can be used to authenticate the key being transferred (through digital
signatures, see section 6.1.4).
Although many cryptographic algorithms have been proposed, only a few
have received wide acceptance and use. An inherent problem in
designing cryptographic algorithms is that such algorithms often rely
on the conjectured intractability of performing certain mathematical
transformations, for instance the factoring of large integers. Such
conjectures are occasionally proven wrong, both due to new algorithms
as well as an unforeseen increase in readily available computing
power.
Here we give a brief account of some algorithms in common use
today. Encryption algorithms belong to one of three main types.
Stream ciphers views the message to be enciphered as a bit
stream. The encrypted message results from performing a bitwise
exclusive-or operation between the message bit stream and a second,
pseudo-random, bit stream. The generation of the second bit stream is
controlled by the encryption key. The receiver deciphers the message by
recreating the second bit stream and x-oring it with the encrypted
message. The main advantage of stream cipher is that encryption and
decryption can be implemented very efficiently.
Block ciphers function differently in that encryption is
performed sequentially on fixed sized chunks of the message, a common
block size is 64 bits.
Asymmetric algorithms have two keys, one which usually is kept
secret while the other is publicized. A message that is encrypted
with the secret key can only be decrypted using the public key, and
vice versa.
Well known encryption algorithms are
- RSA.
- This algorithm was presented by Rivest, Shamir, and
Adleman
[4] (``RSA'') in 1977 [RSA78]. RSA is an
asymmetric algorithm that is widely used, primarily for
authentication and key exchange purposes.
- Diffie-Hellman.
- Named after its inventors, Diffie-Hellman is
not

an

encryption algorithm, but a protocol
that allows two parties to agree on a shared secret without any
prior knowledge and without the need for transferring the secret
itself [DH76].
- DES.
- DES stands for Data Encryption Standard. This
block cipher algorithm was endorsed by the United States Government
as an official standard in 1977 and has since been revised several
times. (The current specification is Federal Information
Processing Standards Publication 46-2 published by the National
Institute of Standards and Technology [Nat93]). DES
is one of the most widely used encryption algorithms in the world.
However, even though DES implementations are available outside
the United States, license to export
software implementing DES from the United States is very rarely given.
- RC2.
- This block cipher is a proprietary algorithm designed by
Ronald Rivest for RSA Data Security. RC2 is designed to be a
replacement for DES and also runs more efficiently than
DES. Software utilizing RC2 that limits the key size to
40 bit is generally approved for export from the United States.
- RC5.
- RC5 is also a proprietary algorithm developed by
Ronald Rivest for RSA Data Security (``RC'' stands for ``Ron's
Code'' or ``Rivest's Cipher'') [Riv95]. In RC5, block
size, key size, and the number of internal iterations (rounds) are
parameterized. This parameterization makes the algorithm very
flexible and allows it to be tuned to a wide range of different
requirements on efficiency and level of security.
- IDEA.
- The International Data Encryption Algorithm is a
block cipher and is the result of a European development project.
IDEA was first proposed by Lai and Massey [LM91].
The IDEA algorithm is patented in the USA and several
European countries but can be used free of charge for non-commercial
purposes.
- RC4.
- This cipher is a proprietary and confidential stream
cipher algorithm of RSA Data Security, designed by Ron Rivest.
- SEAL.
- The Software-optimized Encryption Algorithm (SEAL) was introduced by Rogaway and Coppersmith in 1993
[RC93]. SEAL is a stream cipher designed
for efficient implementation in software.
This list is by no means exhaustive. See for instance
[Sch95] for a more complete enumeration and discussion.
Alterations in a message can sometimes occur spontaneously due to
noise or interference in the communications medium. To detect this, a
message can be protected by attaching a checksum value with the
property that the probability for a distorted message to have a correct
checksum is very low.
However, such schemes cannot offer any protection against
deliberate alteration of a message as anyone changing the message
also can substitute the checksum. The checksum must be protected
to form an electronic signature in order to assure that a
deliberate alteration does not pass unnoticed.
Generation of an electronic signature goes through two stages. To
reduce the size of the signature, a message digest is first
created from the message to be signed. This digest is then encrypted
to form the signature proper. Encryption ensures that only authorized
parties can create a valid signature.
A message digest is created using a one-way hash function. The
digest usually has a fixed length such as 128 bits. Provided the digest has
certain properties, signing the digest is as secure as signing
the entire message.
There are several necessary properties a good message digest should
have. Given a message and a digest, it should not be possible to
find another message (that might be substituted for the original one)
yielding the same checksum. Further, it should not be possible to
find or construct two messages having the the same digest. If this
were possible, it is conceivable that someone with fraudulent intent
could construct two versions of, for instance, a contract, both having
the same checksum.
A hash function having the above properties is said to be
collision free.
Well known examples of message digest algorithms are MD4 and
MD5 proposed by Rivest [Riv91,Riv92]. SHA-1,
published by NIST (the National Institute of Standards and
Technology in the USA), is a digest algorithm based on MD4
[Nat95,Sta94]. Dobertin has shown that MD4 is not collision free [Dob96]. Partial
weaknesses have also been found in MD5 [dBB94].
These flaws cast some doubt as to the robustness of this entire family
of algorithms.
Algorithms designed along new principles are being proposed
(e.g.
[4] [AB96]). However, before new algorithms
can gain acceptance, a long process of scrutiny and testing is
necessary.
Given a message digest, a digital signature is computed by encrypting
the digest using the secret key of the originator. The recipient can
verify the signature by computing the digest for the received message
and comparing it to the digest obtained by deciphering the signature.
Usually public key cryptography is used, although sometimes symmetric
key encryption of the digest is also referred to as signing
it. However, using symmetric cryptography provides no way of settling
a dispute about message contents and thus does not really constitute a
signature. A more proper term for a digest signed with using a symmetric key
algorithm is message integrity code, MIC.
Encrypting the checksum with a key known only to the originator, or
only to the originator and the recipient, in the case of a MIC
being created, assures that the signature cannot be replaced.
A digital signatures scheme requires two functions, a signing function
and a function to check the signature. Most schemes rely on the
existence of two keys. One key, 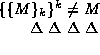 , is used to generate the
signature,
, is used to generate the
signature, 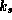 . This key must be kept secret by the
signer at all times, as anyone possessing it can produce a signature.
. This key must be kept secret by the
signer at all times, as anyone possessing it can produce a signature.
The second key,  , is made public. This key is used by anyone
wishing to check a signature relative a message, thus the function
, is made public. This key is used by anyone
wishing to check a signature relative a message, thus the function
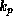 returns true or false. The requirements on
the functions Sign, Check, and the keys
returns true or false. The requirements on
the functions Sign, Check, and the keys 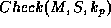 and
and
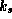 are as follows
are as follows
To meet all of these requirements, a careful choice of
the algorithms for message digest generation and encryption is necessary.
Assume we have signature S and a message M. Further,
assume there is an originator that alone possesses a secret key
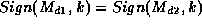 and there is a public key
and there is a public key 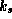 that is known to correspond
to
that is known to correspond
to  . We can then use Check to verify
. We can then use Check to verify

that:

- the signature was produced using
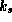
- the signature was produced for the message M
As only the originator has access to 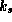 , we can conclude
that the signature was made by her.
Once the identity of the originator has been established we can turn
to the contents of the message.
, we can conclude
that the signature was made by her.
Once the identity of the originator has been established we can turn
to the contents of the message.
A very important application for electronic signatures is for an
issuing authority to sign certificates. Certificates are basically
documents that prove that an identity exists. In order for a
certificate to be trusted it must be possible to verify its origin.
This is done by letting the authority that creates the certificate attach
a signature computed using a secret asymmetric key. Anyone can then
check the authenticity of the certificate using the public key of the
authority.
A complication here is that it can be difficult to obtain guarantees
that a claimed public key indeed is the public key of the issuing
authority. One approach to solving this problem is to create a
hierarchy of certificate authorities where a public key for an
authority is guaranteed by a signature by an authority on a higher
level. At the top of this hierarchy there must be an authority that can be
implicitly trusted (see further section 6.1.5).
As we have seen, cryptographic techniques are available to counter
many security problems stemming from distribution. However, use of
cryptography has its own problems. One example is that laws and export
restriction can hinder international organizations in an effort to
create homogeneous cryptographic environments. Another problematic
factor can be the overhead and performance degradation caused by the
introduction of encrypted or authenticated communications. There are
other problems as well. We concentrate here on a very central
issue, namely that of key distribution.
All cryptography relies on the use of keys. Furthermore, keys must be
kept confidential in order for encryption to provide security. For symmetric
cryptography, the problem of providing both communicating parties with a
common, but secret, key, can be solved by using the Diffie-Hellman key
exchange protocol or through the use of asymmetric cryptography.
However, ensuring confidentiality and proper handling of asymmetric
secret keys is a more difficult problem.
As asymmetric cryptography involves two keys, there are two sides of
the key distribution problem. The confidentiality of the private
(secret) key must be preserved and it must be possible to positively
identify the owner of the public key for authentication purposes.
Conceivably, the integrity of a private key might be compromised at
three stages:
- Upon generation.
- If the system on which key generation takes
places has been compromised, an attacker may eavesdrop and learn
secret keys as they are created. To counter this threat, key
generation should only be performed on a specially dedicated
machine, unconnected to any network, to which physical access is
limited to authorized persons only.
In very sensitive environments, key generation might be set up to
require authorization from two or more security officers in
concert. This reduces the risk for a fraudulent key being created in
a ``legal'' way.
For the issue of keys that will be used to authenticate the
identity of a person, it is paramount that the issuing authority
takes adequate steps to prevent an imposter from obtaining a key
using someone else's identity.
- During distribution.
- Extraordinary care should be taken when
transferring secret keys to nodes in a network. If such transfers
take place over the network, an eavesdropper might intercept the
message and then try to decrypt the message off-line. Due to the
administrative overhead involved, asymmetric key pairs are changed
relatively seldom. Thus it is not unlikely that a dedicated
attacker, given a time span of months or years, might succeed in
decrypting the secret key before it is changed. The most obvious
countermeasure to this threat is to transport the secret key on a
floppy disk delivered by courier. Once the key is installed on the
target system, the disk should be carefully destroyed.
- While in owner's possession.
-
A basic assumption when using asymmetric private keys for
authentication is that the rightful owner will not voluntarily divulge
her key to others.
Storing a secret key on disk in a workstation relies on the security
provided by the operating system of the workstation. However, many
operating systems are not secured against determined
attacks. Furthermore, a private directory, where a user might
place her secret key, is often part of a distributed file
system. Hence, the secret key might end up being transferred over the
network at each use. Even if secret keys are stored locally, this is
not without problems as it forces a user to always use a specific
machine, or to keep a secret key in several places.
A solution to these problems is to store the key on a smart card.
This alleviates the need for storing the secret key on disk
and also allows the user to move between workstations. A
smart card can also include a processor for performing
encryption/decryption. This greatly improves security as there is
no need for the secret key to ever leave the card, or indeed for
there to be a way to extract the key at all.
The problems that arise when using and handling asymmetric public keys
are of a different nature. The main issue here is to be able to
positively associate a public key with its owner. This amounts to
establishing an association between a key and an identity.
Except for very rare cases, a client cannot be expected to have
first-hand knowledge of key/identity associations. Instead
certificates that assert a key/identity association and that
are signed by a certifying authority, CA, are
used. If a client trusts the CA, it can trust the key/identity
association found in the certificate. However, now another problem
arises, how does a client know that the signature on the certificate
is really that of the CA, and not that of an imposter? The
obvious solution is to let the identity of the CA be certified
by another CA, etc. The issue of what should be at the end of a
such certificate chain is not yet fully resolved. Is it really
possible to institute an authority that is intrinsically trusted
by everyone? What would happen if the key of the top level CA was ever compromised?
Another important issue that must be resolved is that of
identity. Assume Alice wants to send a confidential message to her
associate Bob. If Alice knows Bob's public key this is not a problem.
However, if Bob is a new acquaintance, Alice might not know the key.
In this situation Alice might wish for a some sort of directory where
she can learn Bob's key in way similar to how a telephone directory is used.
X.500 is a recommended standard for a global, distributed,
directory service originally published by CCITT [CCI88].
For information on X.500, see for instance
[WR92,WRH92,URLb].
A problem with the global name space provided by X.500 is
that Alice, in our example, must know Bob's distinguished
name, which is a set of hierarchically structured information that
includes fields such as country, organization, organizational unit, and
name. If Alice does not have all this information, she cannot be sure to
find the correct Bob she is looking for. Another problem with the X.500 name space is that it relies on organizations to make
information about its members available. However, many organizations are
reluctant to do this for integrity or business reasons, leaving the
database incomplete.
Other infrastructures for making public keys available have been
proposed. Rivest and Lampson have proposed SDSI --- A Simple
Distributed Security Infrastructure [RL96]. SDSI represents a move from a global name space to a private one.
Each principal independently maintains a mapping between names and
keys of other principals. A different approach is represented by
ongoing work in the Internet community to define SPKI, the
Simple Public Key Infrastructure [URLa]. SPKI does not have any
direct mapping from individuals to keys at all. Instead, SPKI is
an infrastructure designed for Cyberspace, where people meet and form
associations, often without ever meeting in person.



Next: Authentication
Up: Some security techniques
Previous: Some security techniques
matgu@ida.liu.se
 of 40-128 binary bits are common for symmetric
ciphers. When symmetric encryption algorithms are used, the
same key is used both to encipher and decipher a message. The main
advantage of using this technique is that very fast algorithms and
even hardware implementations are available. This means that
communications can be encrypted without imposing a substantial
overhead.
of 40-128 binary bits are common for symmetric
ciphers. When symmetric encryption algorithms are used, the
same key is used both to encipher and decipher a message. The main
advantage of using this technique is that very fast algorithms and
even hardware implementations are available. This means that
communications can be encrypted without imposing a substantial
overhead.

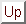


 , is
usually kept secret whilst the other one,
, is
usually kept secret whilst the other one, 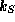 , can be made
public. The keys are so constructed that it is not feasible to derive
the value of one key from the value of the other. Both keys have the
same properties, so which one is kept secret and which is made public is of
no consequence.
, can be made
public. The keys are so constructed that it is not feasible to derive
the value of one key from the value of the other. Both keys have the
same properties, so which one is kept secret and which is made public is of
no consequence.
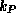 , and the decryption
, and the decryption 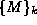 ,
of a message M, using a key k, the properties of the
asymmetric keys
,
of a message M, using a key k, the properties of the
asymmetric keys  and
and 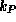 can be expressed as:
can be expressed as: 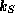 . An important property,
however, is that for any key k of
. An important property,
however, is that for any key k of  and
and 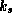 it holds
that
it holds
that 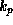 .
.


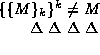 , is used to generate the
signature,
, is used to generate the
signature, 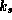 . This key must be kept secret by the
signer at all times, as anyone possessing it can produce a signature.
. This key must be kept secret by the
signer at all times, as anyone possessing it can produce a signature.
 , is made public. This key is used by anyone
wishing to check a signature relative a message, thus the function
, is made public. This key is used by anyone
wishing to check a signature relative a message, thus the function
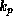 returns true or false. The requirements on
the functions Sign, Check, and the keys
returns true or false. The requirements on
the functions Sign, Check, and the keys 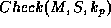 and
and
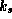 are as follows
are as follows
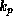 , only
, only 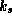 should yield a true result for
should yield a true result for
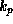 .
.
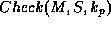 such that
such that 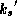
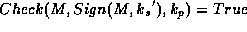 from
from
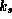 .
.
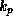 , it should be computationally
infeasible to construct a signature S' for a message
M, such that
, it should be computationally
infeasible to construct a signature S' for a message
M, such that 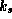 yields True.
yields True.
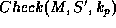 and
and 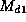 , if
, if
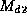 then the probability for
then the probability for 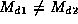 should be smaller than the inverse of
two raised to the number of bits in the signature. That
is, no digest should be more probable than another.
should be smaller than the inverse of
two raised to the number of bits in the signature. That
is, no digest should be more probable than another.
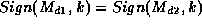 and there is a public key
and there is a public key 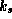 that is known to correspond
to
that is known to correspond
to  . We can then use Check to verify
. We can then use Check to verify 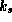
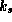 , we can conclude
that the signature was made by her.
Once the identity of the originator has been established we can turn
to the contents of the message.
, we can conclude
that the signature was made by her.
Once the identity of the originator has been established we can turn
to the contents of the message.