1.4 Reliability Modeling

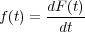
The reliability of a system is typically a function of time and the environment in which the system is operating (Ben-Daya et al. 2009). It is useful to quantify the degradation behavior of the system in terms of its lifetime distribution function, reliability function and corresponding hazard function. A brief introduction to the definition of each of the aforementioned functions, as well as the notation used in this text, is motivated.

Let T be a random variable defining the lifetime of a component with distribution function F(t). If F(t) is a differentiable function, then the probability density function of T is given by

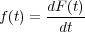(1.1)

The reliability function R(t) of the component is given by

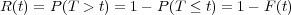(1.2)

In other words, the reliability function R(t) is the probability that the component will be operating after time t, sometimes referred to as the survival probability. The hazard function h(t) is given by

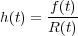(1.3)

The hazard function h(t) describes the rate of change of the conditional probability of failure at time t, and is also referred to as the failure rate. It measures the probability of a component, that has been operating up until time t, to fail in the next unit of time.

1.4.1 Distributions

Several different distributions are in use for life data analysis, for example binomial, lognormal, Poisson, etc. This section will elaborate a bit on the two distributions that are used in this text; the exponential distribution and the Weibull distribution.

Exponential Distribution

The main assumption in the exponential model is that the time between failures is exponentially distributed, i.e. the failures are assumed to occur independent of each other and of time. The probability density function of the exponential distributions is

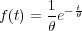(1.4)

where t ≥ 0 and θ > 0. θ is a constant, and also the mean time to failure when the exponential distribution is used to model the time to failure of a system or component. The hazard function becomes a constant

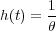(1.5)

Weibull Distribution

The failure rate of all components do not to follow the exponential distribution. Since mechanical parts are exposed to aging and wear mechanisms such as, for example, corrosion and oxidation, they typically exhibit an failure rate that increases with time. The Weibull distribution is more versatile than the exponential distribution, and allows modeling of failure rates that are proportional to a power of time. Depending on the shape parameter, β, its failure rate function can be decreasing, constant or increasing. As such it can be used to model the failure behavior of several real life systems. The probability density function of the Weibull distribution is

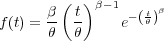(1.6)

where t ≥ 0 and δ,β,θ > 0. θ is the scale parameter, and β is the shape parameter. The corresponding hazard function is given by

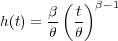(1.7)

β < 1 gives a hazard function that decreases with time, β = 1 gives the exponential distribution with constant hazard function, and β > 1 gives an increasing hazard function with time.

1.4.2 Proportional Hazards Model

The proportional hazard model is one of the most important statistical regression models. Much interest in this model was gained as a result of a paper by Cox (1972), and it has since found many applications in engineering reliability studies as well as biostatistics (K. A. H. Kobbacy et al. 1997; Cox 1972).

The basic assumption for the proportional hazard model is that the hazard function of a part is the product of a baseline function h₀(t), which is dependent on time, and a positive function, ψ(z), which is dependent on explanatory variables, covariates, z_i, i = 1,2,…,n. An extended expression for the proportional hazards model is to include the assumption that the covariates are functions of time as well, as would be the case with recorded historical data such as, for example, environmental data. Each covariate function z_i(t). is then associated with a coefficient, α_i, which gives the following expression for the hazard function

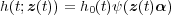(1.8)

where z(t)α = ∑ _i=1ⁿz_i(t)α_i. The column vector α indicates the degree of influence that each covariate has on the hazard function.

A common selection of the relative risk function ψ(z(t)α) is to use the exponential function, due to its simplicity (K. A. H. Kobbacy et al. 1997). In this case, the proportional hazard model takes the form

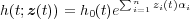(1.9)

It makes intuitive sense that the hazard function becomes identical with the baseline hazard function h₀(t) if the covariates do not affect the system, i.e. α = 0.

The effects of covariates may be to increase or decrease the failure rate. For example, bad operating conditions or incorrectly performed maintenance will increase the failure rate, so that the observed hazard will be higher than the baseline hazard. On the other hand, good operation conditions or improved maintenance practices may lower the failure rate, so that the observed hazard will be lower than the baseline hazard (D. Kumar and Klefsjö 1994). The concept is illustrated in Figure 1.3.

1.4.3 Model Estimation

A traditionally used method to estimate the parameters of a reliability model from failure data is the regression method. The parameters estimated from this method are determined from the slope and y-intercept axis of the straight line that best fits the data. First, an estimate of the lifetime distribution function F(t) must be calculated, for example using median ranks estimation.

The next step is to plot the pairs of points on a probability plot, corresponding to a linearized model of the function of interest. For example, the Weibull model can be linearized by applying the logarithm transformation twice:

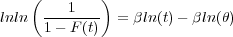(1.10)

From this it is evident that if ln(t) is plotted on one axis, and lnln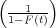 on the other, data distributed according to the Weibull model will plot as a straight line. The shape parameter β is equal to the slope of the straight line, and the scale parameter θ is determined by the location the line crosses the corresponding axis.

Reliability models are generally estimated based on small samples, which makes it difficult to generate good estimates of the lifetime distribution functions. There are alternative approaches to the regression method outlined above, for example, an approach called the maximum likelihood estimation method (Meeker and Escobar 1998).

1.4.4 Uncertainty

Uncertainties can be classified into two categories; aleatory and epistemic. Aleatory uncertainties, also called statistical uncertainties, are unknowns that vary each time an experiment is made, for example, the exact time of failure of a specific component. Epistemic uncertainties, also called systemic uncertainties, arise when the model does not fully match the reality it is intended to simulate. The epistemic uncertainty can be reduced by gaining better knowledge of the modeled system or component, for example, by acquiring larger set of reliability data.

While the aleatory uncertainty of the discussed reliability models is readily addressed by the inherent probability distribution functions, the epistemic uncertainty needs some additional consideration. Calculating the uncertainty of a reliability model parameter θ, involves finding an upper and lower bound θ_min and θ_max such that the following probability is true

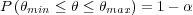(1.11)

where α is the confidence level. There are several ways to estimate the uncertainty associated with θ (Basile and Dehombreux 2007). One approach is to assume that the parameter θ follows the normal distribution, the mean value of which is equal to the estimated parameter :

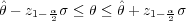(1.12)

where z_p is the p-quantile of the standardized normal distribution, and θ is the estimated standard deviation. A comprehensive description of different methods for uncertainty estimation of model parameters, focusing on the Weibull distribution, can be found in Basile and Dehombreux (2007).