 is then said to dominate
v =
is then said to dominate
v =  if and only if Eq. 1.13 and Eq. 1.14 simultaneously hold
true.
if and only if Eq. 1.13 and Eq. 1.14 simultaneously hold
true.
Maintenance optimization consists of predictive models for chosen performance indicators, selected types of maintenance, an optimization problem formulation and a solution technique (Okasha and Frangopol 2009). This section focuses on the latter; solution techniques for maintenance optimization problems.
If a piece of equipment consists of independent components, the maintenance problem is reduced to a set of single-component problems. However, for a multi-component system that exhibits either economic, stochastic or structural dependence between the components, the optimal maintenance strategy for a single component is not necessarily optimal for the entire system. When more realistic system dynamic behavior is to be considered, the system can no longer be described by analytical models, so one has to resort to simulation techniques (Marseguerra, Zio, and Podofillini 2002). Simulation makes it possible to consider many complex features of maintenance systems that could not be easily included otherwise, for example, redundant components, aging, imperfect repairs and component repair priorities (Márquez 2007). Simulation has been described as the most effective tool for designing and analyzing systems in general and discrete-event systems (e.g. production or logistic systems) in particular (Vin, A. H. Ng, and Oscarsson 2004). Research efforts have been focused on integrating meta-heuristic algorithms, such as genetic algorithms, with simulation software so that “optimal” or close to optimal solutions can be found automatically. Although heuristic optimization methods do not necessarily find the global optimum, they can be applied to find a solution to a complex problem where the true optimum may be difficult to determine. This approach is called simulation-based optimization or simulation optimization, which is perhaps the most important new simulation technology in the last decade (Law and McComas 2002).
A number of computational tools are commonly used for maintenance decision support systems. Some of the tools are analytic hierarchy process, knowledge based analysis, neural networks, fuzzy logic, fuzzy networks, Bayesian theory, and Petri nets (Liyanage et al. 2009). Multi-objective genetic algorithms, Monte Carlo simulation and multi-agent systems have also been applied in maintenance optimization (Marseguerra, Zio, and Podofillini 2002; Kaegi, Mock, and Kröger 2009), and have characteristics that are interesting for the maintenance optimization of remote mobile systems. These three methods (multi-objective genetic algorithms, Monte Carlo simulation and multi-agent systems) will be discussed in further detail in Sections 1.5.2, 1.5.3 and 1.5.4 respectively. However, this section starts off with a discussion about multi-objective optimization in Section 1.5.1.
Single-objective optimization problems is a subset of multi-objective optimization problems. The majority of real life problems involve more than one, often conflicting, criteria. Whenever a decision is to be made on a problem with multiple criteria, simultaneous optimization of multiple criteria takes place. For example, when choosing a hotel to stay at, conflicting criteria can be location, comfort and price. In a general multi-objective optimization problem, there exists no single best solution with respect to all objectives as improving performance on one objective would deteriorate performance of one or more other objectives (Deb, Agrawal, et al. 2001).
A common approach to multi-objective optimization problems is to combine the different criteria using a weighted sum of the conflicting objectives, i.e. a utility function. This approach is simple to apply because by scalarizing an objective vector into a single composite objective function, the problem is converted to a single-objective optimization problem, and thus allows a single optimal solution to be sought using single-objective optimization methods. However, this approach has major drawbacks. One is that the obtained trade-off solution is very sensitive to the utility function, and the utility function is often not well known prior to the optimization process. It can also be difficult to commensurate certain criteria, for example “comfort” and “price”, as used in the hotel selection example above. To provide the decision maker with insight into the characteristics of the problem, the problem should then be treated as a multi-objective problem with non-commensurable objectives. In this way, a number of solutions can be found which provide the decision maker with insight into the characteristics of the problem before a final solution is chosen (Fonseca and Fleming 1993).
Multi-objective optimization seeks to optimize the components of a vector-valued
cost function. Unlike single objective optimization, the solution to this problem is not
a single point, but a set of points known as the Pareto-optimal set. Each point in this
surface is optimal in the sense that no improvement can be achieved in one cost
vector component that does not lead to degradation in at least one of the remaining
components (Fonseca and Fleming 1993). An important concept is that
of non-domination, which can be described assuming , in this example, a
maximization problem. A vector u =  is then said to dominate
v =
is then said to dominate
v =  if and only if Eq. 1.13 and Eq. 1.14 simultaneously hold
true.
if and only if Eq. 1.13 and Eq. 1.14 simultaneously hold
true.
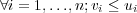 | (1.13) |
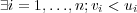 | (1.14) |
Vectors u and v are non-dominated relative each other if neither vector dominates the other. For example, there may be two pairs of elements such that vi < ui and ui+1 < vi+1. Each element in the Pareto-optimal set constitutes a non-dominated solution to the multi-objective optimization problem.
The goal of multi-objective optimization algorithms is to find the entire Pareto-optimal set. However, for many problems, the Pareto-optimal set can be very large, and it can be difficult or infeasible to prove that a particular solution belongs to this set. A heuristic multi-objective optimization algorithm will resort to finding what can be called a “best known Pareto-optimal set”. The set found by the optimization algorithm is itself subject to three criteria, related to the issues discussed above (Zitzler, Deb, and Thiele 2000):
By maintaining a population of solutions, genetic algorithms can search for many non-dominated solutions in parallel. This characteristic makes genetic algorithms very attractive for solving multi-objective optimization problems (Fonseca and Fleming 1993). The ability of a genetic-algorithm to simultaneously search different regions of the solution space makes it possible to find diverse solutions for problems with non-convex and discontinuous solution spaces. Multi-objective genetic algorithms do not require the decision maker to commensurate and weigh the objectives into a utility function, which is one reason that genetic algorithms have been a popular approach to multi-objective design and optimization problems. In the last decade, evolutionary approaches have been the primary tools to solve real-world multi-objective problems (Konak, Coit, and Smith 2006).
An outline of the flow of a generic genetic algorithm is as follows (Konak, Coit, and Smith 2006):
There are several different multi-objective genetic algorithms, for example Niched Pareto Genetic Algorithm (NPGA) (Horn, Nafpliotis, and Goldberg 1994), Region-based Selection in Evolutionary Multi-objective Optimization (PESA-II) (Corne et al. 2001), Strength Pareto Evolutionary Algorithm (SPEA) (Zitzler and Thiele 1999) and Fast Non-dominated Sorting Genetic Algorithm (NSGA-II) (Deb, Pratap, et al. 2002) to mention a few. Many researchers also design their own customized algorithms by combining and adapting strategies from various multi-objective genetic algorithms (Konak, Coit, and Smith 2006). Generally, multi-objective genetic algorithms differ based on their fitness functions, elitism preservation methods, or diversification approaches. Two useful reviews of multi-objective optimization algorithms, that classify the evaluated algorithms according to criteria based on the aforementioned differences, have been made by Zitzler, Deb, and Thiele (2000) and Konak, Coit, and Smith (2006).
Monte Carlo simulation is useful to study the characteristics of systems that are not easily described analytically, for example systems with redundant components, imperfect repairs, etc. The idea behind the Monte Carlo approach is to simulate a large number of system life histories, and use the resulting ensemble of results to estimate the characteristics (such as mean and variance) of the quantities of interest. The values of objective functions can also be determined for each simulated history, and thus for the ensemble. Each simulated history corresponds to a virtual experiment in which the behavior of the system is studied throughout the mission time.
In presence of parameter uncertainty, Monte Carlo simulation can be used for the assessment of the characteristics of a system through the use of so called “double-randomization”. The general idea is to acquire a number of realizations from the multi-dimensional vector of parameters. The realizations are sampled from the multivariate distribution describing the uncertainty of the parameters. For each realization, i.e. vector of parameter values, a number of system histories are simulated using Monte Carlo simulation. Once simulation results have been acquired from all realizations, the collected results are analyzed to find ensemble estimates of the characteristics of the output quantities of interest. In other words, the randomization of the parameters are being superposed to the inherent randomness of the stochastic model. This technique was applied by Marseguerra, Zio, and Podofillini (2004) to study availability and reliability characteristics of a nuclear safety system.
Monte Carlo simulation is widely applied to study models that are infeasible to describe analytically. Both aleatory and epistemic uncertainty can be addressed by the use of the double-randomization technique, which makes Monte Carlo simulation exceptionally useful for reliability modeling purposes. A thorough discussion on the statistical methods of Monte Carlo simulation is available in the book by Robert and Casella (2004).
There does not appear to be a common definition of agent in the literature. In this text, the following definition of objects and agents are used (Kaegi, Mock, and Kröger 2009):
A multi-agent system is a distributed artificial intelligence system in which several interacting, intelligent agents pursue some set of goals or perform some set of tasks (Weiss 2000). Intelligent agents should have the following properties (Lim and Zhang 2003):
An agent specification framework must be capable of capturing the aspects of beliefs the agents have; ongoing interaction that agents have with their environment; goals that agents will try to achieve; and actions that agents perform and the effects of these actions.
Lim and Zhang (2003) has successfully integrated process planning and production scheduling using an approach based on multi-agent systems. Kaegi, Mock, and Kröger (2009) have looked into the feasibility of applying an agent-based approach to maintenance strategy modeling and optimization, and conclude that agent-based modeling, combined with other modeling and simulation techniques (hybrid modeling approach), has a high potential to realistically model large and complex maintenance solutions. Multi-agent systems thus appears to be a promising approach to the modeling and simulation of maintenance organizations, including those aimed at remote and distributed systems.